Area
Area är ett matematiskt begrepp som används för att mäta storleken på en yta eller ett område. Vi kan till exempel beräkna arean på en tvådimensionell figur såsom en kvadrat, rektangel, triangel eller cirkel. Till vardags har du säkert hört någon prata om area när det kommer till hur stort ett hus eller en tomt är!
I den här guiden går vi igenom hur du gör räknar ut arean på en rektangel, en kvadrat och en triangel. Längre ner hittar du även uppgifter som du kan använda för att öva!
Så gör du för att beräkna area
Metoden vi använder för att beräkna en area beror på vad vi har för sorts figur. De två vanligaste figurerna som vi behöver kunna räkna ut arean av är rektanglar och trianglar. Kvadraten går under samma kategori som rektangeln! Arean mäts alltid i kvadratenheter och betecknas med cm2, dm2, m2 och km2. Oavsett vilken enhet du använder börjar vi ordet med kvadrat. 1 cm2 sägs alltså som “1 kvadratcentimeter”.
Räkna ut arean av en rektangel
Arean av en rektangel följer sambandet:
Arean={basen}\cdot{h\"ojden}, vilket ofta skrivs som A={b}\cdot{h}.
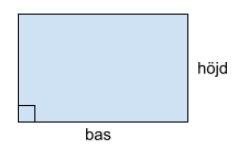
Basen är längden av rektangelns vågräta sida, alltså sidan som går i sidled. Höjden är längden av rektangelns lodräta sida, alltså sidan som går uppåt.
När vi beräknar en kvadrats area använder samma formel, alltså
{basen}\cdot{h\"ojden}. I det fallet är dock basen=h\"ojden eftersom att alla sidor i en kvadrat är lika långa. Vi kan därför även säga att vi tar sidan upphöjt i två!
Exempel – rektangelns area
Låt oss säga att vi har en rektangel med mått enligt bilden. Vi vill beräkna figurens area.
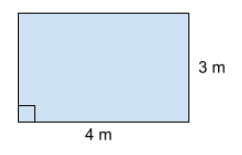
Vi ser att basen är sidan som är 4 m lång och att höjden är sidan som är 3 m lång. Vi börjar med att sätta in våra värden för basen och höjden i sambandet
Arean={basen}\cdot{h\"ojden}. Vi får att:
Arean={basen}\cdot{h\"ojden}= {4}\cdot{3}=12m^2Rektangelns area är 12m^2.
Räkna ut triangelns area
Arean av en triangel beräknar vi på ett liknande sätt. Det följer sambandet
Arean=\frac{{basen}\cdot{h\"ojden}}{2}I en rätvinklig triangel (en triangel med en 90° vinkel) är basen längden av triangelns vågräta sida, alltså sidan som går i sidled. Höjden är längden av triangelns lodräta sida, alltså sidan som går uppåt.
Basen och höjden är alltså de två sidorna som ligger intill den räta vinkeln. Den räta vinkeln markeras med en ruta.
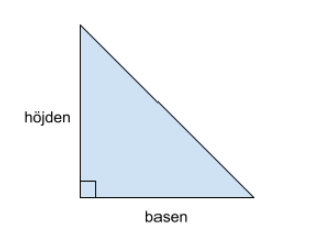
Triangelns area är exakt hälften av arean av en rektangel med samma höjd och bas. Det är därför vi delar {basen}\cdot{h\"ojden} med 2 för att få arean.
Vi vet att triangelns area måste vara hälften av rektangelns area eftersom vi kan bilda en rektangel med samma mått som triangeln genom att placera en kopia av triangeln bredvid sig själv.
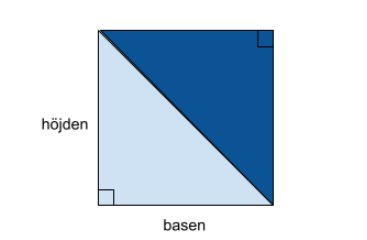
Det betyder att triangelns area är exakt hälften så stor som rektangelns area.
Exempel – triangelns area
Låt oss säga att vi har en triangel med mått enligt bilden. Vi vill beräkna arean av figuren.
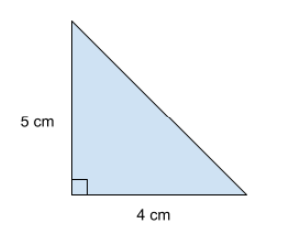
Vi ser att vi har 4 cm som bas och 5 cm som höjd. Vi sätter in detta i sambandet
Arean=\frac{{basen}\cdot{h\"ojden}}{2}.
Arean=\frac{{basen}\cdot{h\"ojden}}{2}= \frac{{4}\cdot{5}}{2}Vi beräknar först produkten (multiplikationen) i täljaren (termen som är överst i bråket). Sedan delar vi med 2.
\frac{{4}\cdot{5}}{2}= \frac{20}{2}= 10cm^2Triangelns area är 10 cm2.
Räkna ut triangelns area utan en rät vinkel
När triangeln inte är rätvinklig har vi samma bas, men höjden mäter vi på ett lite annat sätt. Höjden sätter vi då som sträckan från basen till triangelns topp. Höjden sitter nu på triangelns insida, istället för dess kant.
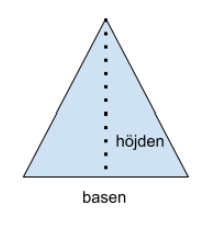
Höjden är alltså den streckade linjen som går längs triangelns mitt.
Exempel – area av en triangel utan en rät vinkel
Låt oss säga att vi har en icke rätvinklig triangel med mått enligt bilden. Vi vill beräkna arean av figuren.
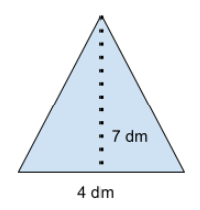
Vi har 4 dm som bas och 7 dm som höjd. Vi använder samma samband som tidigare:
Arean=\frac{{basen}\cdot{h\"ojden}}{2}.
Arean=\frac{{basen}\cdot{h\"ojden}}{2}= \frac{{4}\cdot{7}}{2}Vi beräknar produkten i täljaren först.
\frac{{4}\cdot{7}}{2}= \frac{28}{2}= 14dm^2Arean av triangeln är 14dm^2.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Räkna ut arean av följande rektangel. Svara i m^2.
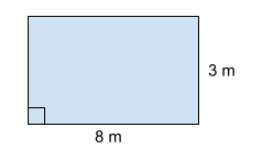
Svarsalternativ 1: 18m^2
Svarsalternativ 2: 20m^2
Svarsalternativ 3: 24m^2
Svarsalternativ 4: 30m^2
Fråga 2: Beräkna arean av triangeln. Svara i cm^2.
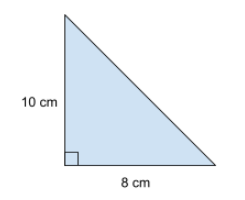
Svarsalternativ 1: 24cm^2
Svarsalternativ 2: 30cm^2
Svarsalternativ 3: 32cm^2
Svarsalternativ 4: 40cm^2
Fråga 3: Beräkna arean av triangeln. Svara i dm^2.
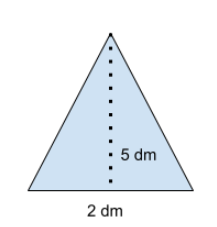
Svarsalternativ 1: 5dm^2
Svarsalternativ 2: 8dm^2
Svarsalternativ 3: 10dm^2
Svarsalternativ 4: 15dm^2
Tips från Fredrik
Därför ska du lära dig beräkna rektangelns area

När du har lärt dig hur du räknar ut arean på en rektangel och en triangel blir det helt plötsligt lättare att räkna ut arean på alla möjliga former! I vardagen möter du ofta former som kanske inte är perfekta kvadrater eller rätvinkliga trianglar. Dessa komplexa former kan verka utmanande men det finns en smart strategi. Du kan bryta ned dem i enklare delar som du känner igen! Till exempel kan en parallelltrapets omvandlas till en rektangel med två trianglar på sidorna. Genom att ha koll på hur man beräknar area för rektanglar och trianglar blir du en riktig mästare i att räkna ut storleken på ytor, oavsett hur knepiga formerna kan se ut!
Det är alltså väldigt viktigt att först lära sig hur man beräknar arean på rektanglar och trianglar. Känns det knepigt? Oroa dig inte! Allakandos studiecoacher är experter på matte och hjälper dig gärna bemästra area och andra matematiska problem!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

