Tips för att räkna med Pythagoras sats
Pythagoras sats är en mycket användbar mattematisk formel som gäller endast en rätvinklig triangel. Att triangeln är rätvinklig innebär att den har en vinkel som är 90°. En rät vinkel markeras alltid med en liten ruta (□). Ser du denna ruta i en triangel vet du alltså att vi kan använda oss av Pythagoras sats.
I den här guiden har vi samlat instruktioner och tips för hur du använder Pythagoras sats. Längre ner kan du även hitta uppgifter att jobba med för att öva in formeln!
Så räknar du ut Pythagoras sats
Hypotenusan i kvadrat är enligt pythagoras sats lika med summan av kvadraterna av kateterna. Låter det krångligt? Ingen fara, låt oss gå igenom det steg för steg!
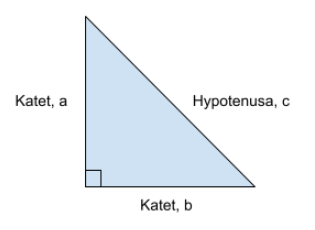
De två sidorna som ligger bredvid den räta vinkeln (rutan) kallar vi för kateter. Vi ger dem beteckningarna a och b. Sidan som ligger längst ifrån den räta vinkeln (rutan) kallar vi för hypotenusan, vilket vi ger beteckningen c.
Enligt Pythagoras sats finns följande samband för sidorna i rätvinkliga trianglar:
a^2+b^2=c^2A och b är längden på kateterna och c är längden på hypotenusan. Det spelar ingen roll vilken av de två kateterna vi sätter som a respektive b.
Pythagoras sats och vinklar
Om du känner till längden på två av sidorna i en rätvinklig triangel, kan du använda Pythagoras sats för att beräkna längden på den tredje sidan. För att göra det, kvadrerar du längden på de kända sidorna, adderar dem och tar sedan roten av summan för att få längden på den okända sidan.
Pythagoras sats kan också användas för att avgöra om en triangel är rätvinklig. Om summan av kvadraterna av de två kortaste sidorna är lika med kvadraten av den längsta sidan, då har triangeln en rät vinkel och är därmed en rätvinklig triangel.
Här hittar du vår guide till likbenta trianglar!
Koordinatsystem och pythagoras sats
Geometriska tillämpningar av Pythagoras sats sträcker sig långt bortom enbart trianglar och kan till och med vara centrala för att lösa problem i ett koordinatsystem. Ett av de mest användbara exemplen på detta är när man behöver beräkna avståndet mellan två punkter i ett koordinatsystem.
I ett tvådimensionellt koordinatsystem representeras punkter av sina koordinater (x, y). Om vi har två punkter A med koordinater (x1, y1) och B med koordinater (x2, y2), kan avståndet mellan dem beräknas med hjälp av Pythagoras sats.
För att förstå detta, kan vi tänka på avståndet mellan punkterna A och B som hypotenusan i en rätvinklig triangel. De två kateterna skulle då vara de horisontella och vertikala avstånden mellan punkterna.
Den horisontella skillnaden mellan x-koordinaterna representerar längden på ena kateten, och den vertikala skillnaden mellan y-koordinaterna representerar längden på den andra kateten. Sedan kan vi använda Pythagoras sats för att beräkna längden på hypotenusan, vilket i detta fall motsvarar avståndet mellan punkterna A och B.
Matematiskt uttryckt blir detta:
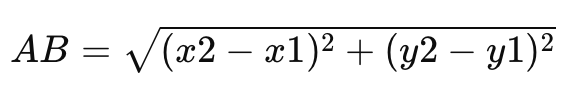
Där AB är avståndet mellan punkterna A och B, och x1x1, y1y1 är koordinaterna för punkt A, medan x2x2, y2y2 är koordinaterna för punkt B.
Läs mer om koordinatsystem här!
Räkneexempel med Pythagoras sats
Prova sambandet
Vi kan nu testa sambandet på en rätvinklig triangel med sidorna 3 cm, 4 cm och 5 cm.
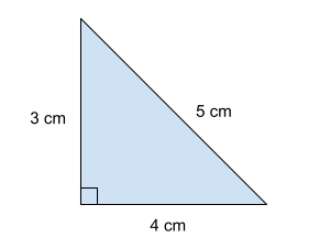
Sidorna som ligger intill den räta vinkeln (rutan) är kateter. Kateterna, som vi kallar för a och b, är alltså 3 cm respektive 4 cm långa. Hypotenusan, som vi kallar för c, är 5 cm lång. Vi sätter in det i vår ekvation a^2+b^2=c^2 och får att 3^2+4^2=5^2.
När vi har ett tal upphöjt till 2 innebär det att vi multiplicerar talet med sig självt. Det innebär alltså att 3^2={3}\cdot{3}=9.
Vi vill nu se om sambandet stämmer genom att undersöka om vänsterled (uttrycket till vänster om likamedtecknet) är lika med högerled (uttrycket till höger om likamedtecknet). Vi förenklar vänsterled på följande vis:
3^2+4^2= {3}\cdot{3}+{4}\cdot{4}= 9+16= 25Sedan förenklar vi högerled:
5^2= {5}\cdot{5}= 25Vi har alltså visat att vänsterled 3^2+4^2 är lika med högerled 5^2 och därmed att sambandet 3^2+4^2=5^2 stämmer.
Så gör du när hypotenusan är okänd
Om vi vet längden av två sidor i en rätvinklig triangel kan vi alltid räkna ut längden av den tredje sidan med hjälp av Pythagoras sats.
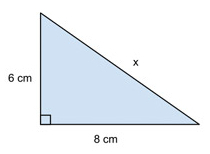
Låt oss säga att vi har en rätvinklig triangel med sidlängderna 6 cm och 8 cm enligt bilden. Den tredje sidan är dock okänd och vi kallar den för x. Vi vill ta reda på längden av den okända sidan.
Vi vet att våra två sidor 6 cm och 8 cm är kateter eftersom de ligger intill den räta vinkeln. Det innebär att c är hypotenusan. Vi sätter in kateternas värden i ekvationen a^2+b^2=c^2 och får att 6^2+8^2=c^2.
Vi börjar med att förenkla vänsterled.
6^2+8^2= {6}\cdot{6}+{8}\cdot{8}= 36+64= 100Alltså gäller att 100=x^2. När vi löser ut en variabel, som x, vill vi alltid att den ska stå ensamt. Vi vill alltså skriva om x^2 till endast x, vilket vi kan göra genom att ta kvadratroten ur båda sidorna.
x^2=100 x=\sqrt{100}=10Vi får alltså att x och hypotenusans längd är 10 cm. Var noga med att inte glömma enheten när du anger svaret.
Så gör du när en kateter är okänd
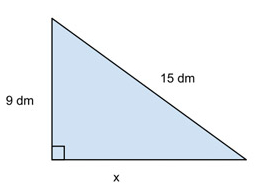
Det behöver inte alltid vara hypotenusan som är den obekanta sidan i triangeln. Låt oss säga att vi har en rätvinklig triangel med sidlängderna 9 dm och 15 dm enligt bilden. Vi vill ta reda på längden av den okända sidan. Eftersom att vi vet att triangeln är rätvinklig kan vi använda oss av Pythagoras sats.
Vi kallar den okända sidan för x. Sidorna 9 dm och x står intill den räta vinkeln, vilket betyder att de är kateter a och b. Sidan 15 dm är hypotenusan och vi kallar den för c. Vi sätter in det i ekvationen a^2+b^2=c^2 och får att 9^2+x^2=15^2.
Vi börjar med att förenkla termerna där vi har siffror, alltså 9^2 och 15^2.
9^2+x^2=15^2 {9}\cdot{9}+x^2={15}\cdot{15} 81+x^2=225Sedan subtraherar vi båda leden med 81. Det gör så att termen 81 flyttas över till andra sidan likamedtecknet och då kommer x^2 att stå ensamt.
81+x^2-81=225-81 x^2=144Vi tar nu roten ur båda sidorna för att skriva om x^2 till endast x.
x=\sqrt{144}=12Vi får alltså att x är 12 dm.
Övningsuppgifter
Frågor med svarsalternativ för att öva Pythagoras sats:
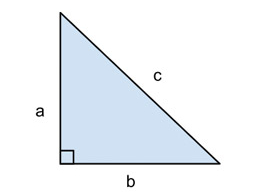
Fråga 1: Vilka sidor är kateter i den rätvinkliga triangeln?
Svarsalternativ 1: a och b
Svarsalternativ 2: b och c
Svarsalternativ 3: a och c
Svarsalternativ 4: Endast c
Korrekt svar: a och b
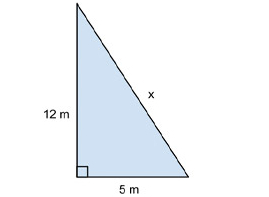
Fråga 2: Vad är längden av sidan x?
Svarsalternativ 1: 7 m
Svarsalternativ 2: 10 m
Svarsalternativ 3: 11 m
Svarsalternativ 4: 13 m
Korrekt svar: 13 m
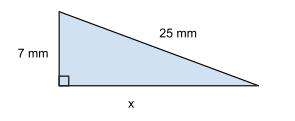
Fråga 3: Vad är längden av sidan x?
Svarsalternativ 1: 16 mm
Svarsalternativ 2: 17 mm
Svarsalternativ 3: 20 mm
Svarsalternativ 4: 24 mm
Korrekt svar: 24 mm
Fredriks tips
Hur du lär dig Pythagoras sats

Innan du dyker djupare in i Pythagoras sats är det viktigt att du förstår de grundläggande begreppen. Se till att du vet hur man identifierar rätvinkliga trianglar och att du vet vilken av sidorna som är hypotenusan samt vilka kateterna är. Det är också bra att känna till hur du räknar upphöjt i och roten ur.
Är du säker på alla delar av en rätvinklig triangel blir det lätt att veta när du kan använda formeln och vilka sidor som byter ut vilken bokstav. Om du dessutom redan är säker på exponenter och kvadratroten blir Pythagoras sats inga problem att räkna på!
Skulle du vilja ha hjälp på traven med Pythagoras sats, eller någon annan del av matematiken, har vi studiecoacher som mer än gärna ställer upp. Tillsammans ser vi till att du besegrar matten!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Läxhjälp i alla ämnen
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

