Sinus
Vi har i tidigare avsnitt gått igenom trigonometri som helhet och lärt oss betydelsen av sinus, cosinus och tangens. Där har vi även lärt oss om de olika sidorna i en rätvinklig triangel och vad de innebär. I det här avsnittet kommer vi lära oss mer om sinusfunktionen och hur vi använder den. Längre ner hittar du även uppgifter du kan använda för att öva!
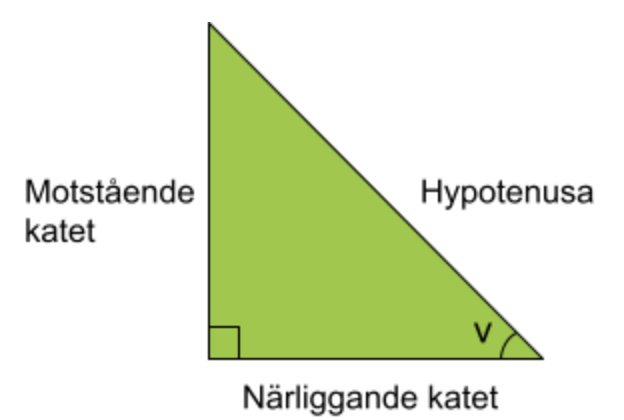
Sinusfunktionen beskriver sambandet mellan en vinkel, dess motstående katet och hypotenusan i en rätvinklig triangel:
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}För varje vinkel v finns ett visst värde på sinus. Detta värde är alltså lika med längden av vinkelns motstående katet delat på längden av triangelns hypotenusa. Värdet av sinus vid en viss vinkel får vi lättast fram med hjälp av vår miniräknare.
Enhetscirkeln kan användas för att tolka sinusvärden för vinklar som inte är associerade med trianglar.
Så räknar du med sinus
För varje given vinkel motsvarar sinus ett specifikt värde. Detta värde definieras som förhållandet mellan längden av hypotenusan och längden av den motstående kateten.
Om vi har värdet på vinkeln v och antingen den motstående kateten eller hypotenusan så kan vi ta reda på längden av den återstående sidan med hjälp av sinus.
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}Nedan ser vi ett exempel på hur vi kan använda sinus för att bestämma längden av en sida i en rätvinklig triangel.
Exempel: Bestäm längden av sidan a. Svara i centimeter (cm). Avrunda till en decimal.
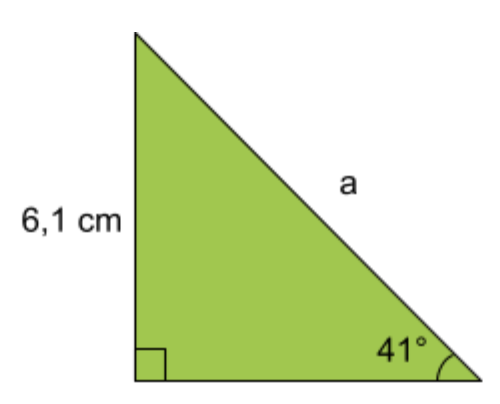
Svar: 9,3\;cm
Lösning: Vi har värdet på en vinkel, som är 41^\circ, och längden av en katet, som är 6,1\;cm. Sett utifrån den 41-gradiga vinkelns perspektiv är kateten med längden 6,1\;cm en motstående katet. Den obekanta sidan, a, är hypotenusan i triangeln.
Vi använder oss av sinus eftersom vi vet vinkeln och längden av den motstående kateten, men vill ta reda på längden av hypotenusan.
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}Vi sätter in värdena för vår vinkel och den motstående kateten. Vi ersätter även hypotenusan med a.
sin\;41^\circ=\frac{6,1}{a}Vi vill att a ska stå ensamt på sin sida om likamedtecknet, men vi vill först se till att kvoten i höger led försvinner. Därför multiplicerar vi båda leden med a, vilket gör så att a flyttas över från nämnaren i höger led till vänster led.
{sin\;41^\circ}\cdot{a}={\frac{6,1}{a}}\cdot{a} {sin\;41^\circ}\cdot{a}=6,1Vi ser nu att det blir lättast att isolera a i vänster led eftersom vi kan uppnå detta genom att dela båda sidor med sin\;41^\circ.
\frac{{sin\;41^\circ}\cdot{a}}{sin\;41^\circ}=\frac{6,1}{sin\;41^\circ} \frac{6,1}{sin\;41^\circ}=aNu bestämmer vi värdet av sin\;41^\circ med hjälp av vår miniräknare.
sin\;41^\circ\approx0,65606Vi sätter in värdet av sin\;41 i ekvationen a=\frac{6,1}{sin\;41^\circ}.
a=\frac{6,1}{0,65606}Vi beräknar nu värdet av kvoten \frac{6,1}{0,65606} i höger led.
a=\frac{6,1}{0,65606}= 9,29794\;cmVi avrundar till en decimal och får att sidan a har längden 9,3\;cm.
När man bestämmer sinus för vinkeln v är oftast det smidigaste att använda sinusfunktionen på vår miniräknare, men det behöver vi inte. Sinus har nämligen ett exakt värde för vissa vinklar som vi kan använda istället. Nedan ser du några exakta värden för sinus.
sin\;0^\circ=0 sin\;30^\circ=\frac{1}{2} sin\;45^\circ=\frac{1}{\sqrt{2}} sin\;60^\circ=\frac{\sqrt{3}}{2} sin\;90^\circ=1Nedan ser vi ett exempel på hur vi kan använda det exakta värdet för sinus när vi bestämmer längden av en sida.
Exempel: Bestäm längden av sidan x. Svara i millimeter (mm). Avrunda till heltal.
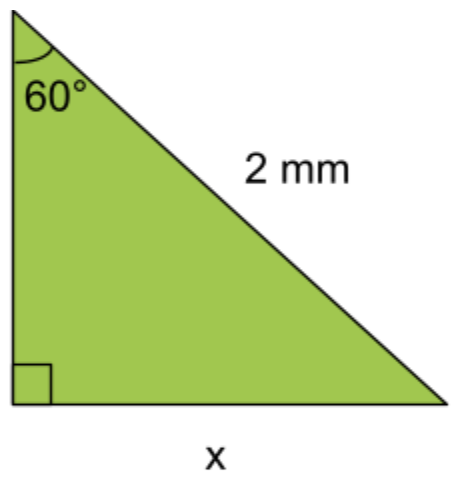
Svar: 1,7\;mm
Lösning: Vi har värdet på en vinkel, som är 60^\circ, och längden av hypotenusan som är 2\;mm. Vi vill ta reda på längden av sidan x, som är motstående katet sett från den 60-gradiga vinkelns perspektiv.
Vi använder oss av sambandet för sinus för att ta reda på längden av sidan x.
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}Vi börjar med att sätta in värdena för vår vinkel och hypotenusan. Vi ersätter även den motstående kateten med x.
sin\;60^\circ=\frac{x}{2}Vi vill bestämma värdet av x. Därför vill vi att x ska stå ensamt till höger om likamedtecknet. Vi flyttar över 2 så att x kan stå ensamt, vilket vi gör genom att multiplicera båda sidorna med 2.
sin\;60^\circ=\frac{x}{2} {sin\;60^\circ}\cdot{2}=\frac{x}{2}\cdot{2} {sin\;60^\circ}\cdot{2}=xNu behöver vi endast bestämma ett värde på uttrycket {sin\;60^\circ}\cdot{2}. Vi börjar med att hitta värdet för sin\;60^\circ.
Vi ser i tabellen ovanför exemplet att sin\;60 har ett exakt värde som är lika med \frac{\sqrt{3}}{2}. Vi ersätter sin\;60 med \frac{\sqrt{3}}{2} i ekvationen.
x={sin\;60^\circ}\cdot{2} x={\frac{\sqrt{3}}{2}}\cdot{2}Vi kan förenkla bort tvåorna eftersom \frac{2}{2}=1.
x=\sqrt{3}\approx 1,73205\;mmVi avrundar till en decimal och får att längden av sidan x är 1,7\;mm.
Om vi har värdet på hypotenusan och en av de två kateterna i en rätvinklig triangel, så kan vi ta reda på värdet av en av vinklarna genom att använda den inversa sinusfunktionen. Den inversa sinusfunktionen skrivs som sin^{-1} eller arcsin.
Precis som med den vanliga sinusfunktionen så finns den inversa sinusfunktionen inprogrammerad i din miniräknare.
Om vi har en ekvation där vi vill ta reda på vinkeln v, som exempelvis sin\;v=\frac{2}{3}, så kan vi lösa den genom att ta den inversa funktionen av sinus båda sidorna.
sin\;v=\frac{2}{3} sin^{-1}(sin\;v)=sin^{-1}\frac{2}{3}Termerna sin^{-1} och sin tar ut varandra i vänster led. Kvar blir vinkeln v.
v=sin^{-1}\frac{2}{3}Vi behöver nu endast bestämma värdet av uttrycket i höger led, sin^{-1}\frac{2}{3}, vilket vi gör med vår miniräknare.
v=sin^{-1}\frac{2}{3}\approx 42^\circVi får att vinkeln v är ungefär 42^\circ.
Exempel: Beräkna värdet av vinkeln v. Svara i hela grader.
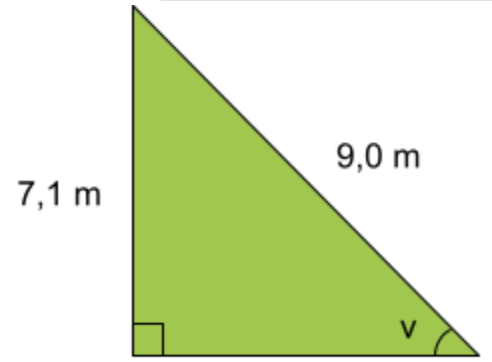
Svar: 52^\circ
Lösning: Vi har längden av en katet, som är 7,1\;m, och längden av hypotenusan, som är 9,0\;m. Sett utifrån vinkeln v:s perspektiv är den 9,0\;m långa kateten en motstående katet.
Vi vet alltså den motstående kateten och hypotenusan, men inte vinkeln. Vi kan därmed använda sinus för att bestämma vinkeln v.
sin\;v=\frac{motst{\aa}ende\;katet}{hypotenusa}Vi sätter in längderna av den motstående kateten och hypotenusan i sambandet.
sin\;v=\frac{7,1}{9}Vi vill att v ska stå ensamt i vänster led, alltså vill vi flytta över sinus från vänster led till höger led. Vi använder därför den inversa sinusfunktionen, som skrivs sin^{-1}, på båda sidor.
sin^{-1}(sin\;v)=sin^{-1}\frac{7,1}{9}Termerna sin^{-1} och sin tar ut varandra i vänster led. Kvar blir vinkeln v.
v=sin^{-1}\frac{7,1}{9}Vi beräknar nu värdet av sin^{-1}\frac{7,1}{9} på vår miniräknare.
v=sin^{-1}\frac{7,1}{9}\approx 52,08^\circVi avrundar till hela grader och får att vinkeln v är 52^\circ.
Övningsuppgifter
Frågor med svarsalternativ:
Fråga 1: Bestäm längden av sidan x. Svara i centimeter (cm). Avrunda till en decimal
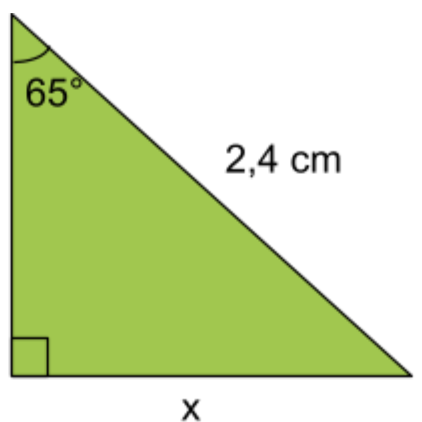
Svarsalternativ 1.1: 2,2\;cm
Svarsalternativ 1.2: 2,5\;cm
Svarsalternativ 1.3: 2,9\;cm
Svarsalternativ 1.4: 3,1\;cm
Korrekt svar: 2,2\;cm
Fråga 2: Bestäm längden av sidan x. Svara i decimeter (dm). Avrunda till heltal.
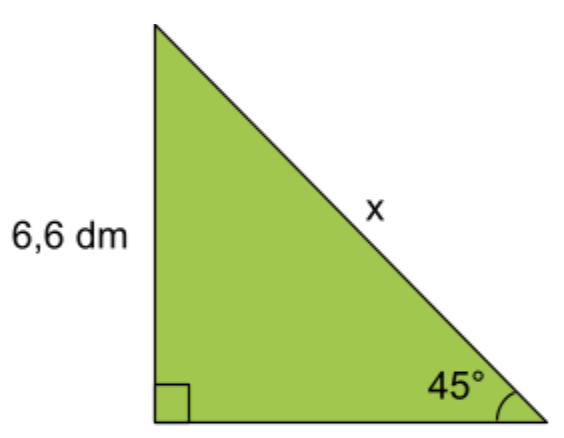
Svarsalternativ 2.1: 9\;dm
Svarsalternativ 2.2: 10\;dm
Svarsalternativ 2.3: 12\;dm
Svarsalternativ 2.4: 13\;dm
Korrekt svar: 9\;dm
Fråga 3: Beräkna värdet av vinkeln v. Svara i hela grader.
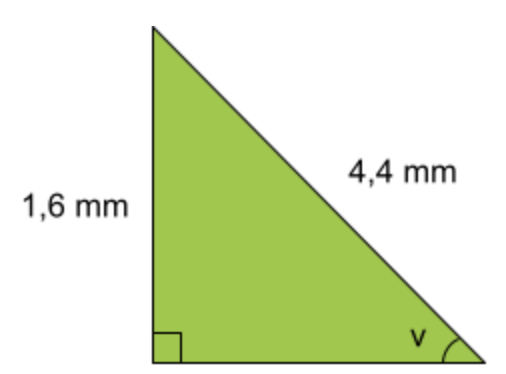
Svarsalternativ 3.1: 21^\circ
Svarsalternativ 3.2: 24^\circ
Svarsalternativ 3.3: 33^\circ
Svarsalternativ 3.4: 36^\circ
Korrekt svar: 21^\circ
Fredrik tipsar
Lär dig räkna med sinus

Trigonometriska funktioner såsom sinus, cosinus och tangens kan verka väldigt komplicerade till en början. Med rätt grunder och mycket övning kommer du att bemästra även dem – bara du verkligen vill det!
En användbar strategi är att memorera värden för sinus vid vanliga vinklar som 0°, 30°, 45°, 60° och 90°. Detta kommer att göra dina beräkningar lättare och mycket smidigare. Skriv gärna ner dem i en lathund att ha i matteboken eller nära till hands när du pluggar så kan du dem snart utantill!
Ett annat tips är att använda visuella hjälpmedel såsom enhetscirkeln. Med hjälp av den kan du lättare se sambandet mellan vinklar och trigonometriska funktioner.
Känner du att trigonometrin fortfarande känns klurigt? På Allakando har vi pedagogiska studiecoacher som gärna hjälper dig med matten. De kan erbjuda förklaringar, övningar och användbara tips som gör matematiken både enklare och roligare!

Fredrik Fridlund, VD & Grundare
Har själv undervisat över 3 000 elever sedan 2007
Så hjälper Allakando dig till toppresultat i skolan

Mattehjälp för alla nivåer
Slipp stressen och höj betygen med en personlig studiecoach! Allakando har över 15 års erfarenhet och hjälper varje år 26 000+ elever.

Effektiva kurser som höjer betygen
Lär dig hela nästa års matte på bara fem halvdagar, kom förbered till nationella proven och mycket mer!

Allt du behöver inför högskoleprovet
Plugga på tusentals uppgifter med förklaringar, videofilmer och guider i vår webbkurs. Gå en intensivkurs eller få en personlig HP-coach!

