Sammanfattning av nationella provet i matte 2

Alla elever som läser matte 2a, 2b eller 2c skriver tre delprov. Utöver ämnesplanen för 2a, läser 2b och 2c även exempelvis algebra, budgetering, likformighet, ekvationssystem, statistik samt exponentialfunktioner och logaritmer. Vi har samlat allt här på ett ställe så att du kan ha koll på vad som kan komma upp på nationella provet i matte 2!

/Fredrik Fridlund på Allakando

Sammanfattning av nationella provet i matte 1

Algebra & Ekvationer

Parenteser

En parentes

När man multiplicerar en term med en parentes måste man multiplicera båda talen i parentesen.

Exempel: Förenkla uttrycket $4 x(2 x+9)$

Två parenteser

När man multiplicerar två parenteser med varandra multiplicerar man ”alla med alla”.

$(a+b)(c+d)=a c+a d+b c+b d$ ‎

Kvadreringsreglerna

$(a+b)^{2}=a^{2}+2 a b+b^{2}$ ‎

$(a-b)^{2}=a^{2}-2 a b+b^{2}$ ‎

Konjugatregeln

Det är viktigt att även kunna dessa regler från höger till vänster, alltså baklänges, då det är ett bra redskap när man faktoriserar.

(a+b)(a-b)=a^{2}-b^{2}

Faktorisera

Att faktorisera betyder att man skapar faktorer, alltså skapar gångertecken. Det vanligaste tillvägagångssättet är att man bryter ut en faktor, men ibland kan man använda konjugat‐ eller kvadreringsregeln baklänges.

Exempel: Faktorisera uttrycket $24 x-6 x^{2}$

24 x-6 x^{2} = 4 \cdot {\color{#96C933} 6 x}-{\color{#96C933} 6x} \cdot x = {\color{#96C933} 6x}(4-x)

Bryta ut/faktorisera är motsatsen till att multiplicera in i en parentes. Därför kan vi kontrollräkna vårt svar genom att multiplicera in i parentesen igen.

Faktorisera med konjugat‐ och kvadreringsregeln

När man ska faktorisera ett uttryck och det inte finns någon gemensam faktor kan man testa att använda antingen konjugatregeln eller kvadreringsregeln baklänges.

Exempel: Faktorisera uttrycket $81-x^{2}$ .

Då vi har två kvadrater med ett minustecken emellan kan

vi använda konjugatregeln för att faktorisera:

$\begin{aligned} 81-x^{2}=&{\color{#96C933} 9}^{2}-{\color{#3396C9} x}^{2}=({\color{#96C933} 9}+{\color{#3396C9} x})({\color{#96C933} 9}-{\color{#3396C9} x})\\ & {\color{#96C933} a}^{2}-{\color{#3396C9} b}^{2}=({\color{#96C933} a}+{\color{#3396C9} b})({\color{#96C933} a}-{\color{#3396C9} b}) \end{aligned}$ ‎

Exempel: Faktorisera och förenkla uttrycket $\frac{x^{2}-4 x+4}{2 x-4}$

Uttrycket $x^{2}-4 x+4$ har ingen gemensam faktor, så vi har inget vi kan bryta ut. Vi kan däremot faktorisera med kvadreringsregeln.

$\begin{aligned} x^{2}-4 x+4= & {\color{#96C933} x}^{2}-2 \cdot {\color{#96C933} x} \cdot {\color{#3396C9} 2}+{\color{#3396C9} 2}^{2}=({\color{#96C933} x}-{\color{#3396C9} 2})^{2} \\ & {\color{#96C933} a}^{2} \; -\; 2 {\color{#96C933} a} {\color{#3396C9} b}\;+\; {\color{#3396C9} b}^{2}\;=({\color{#96C933} a}-{\color{#3396C9} b})^{2} \end{aligned}$ ‎

$\begin{aligned}\text{Svar:} \quad \frac{x^{2}-4 x+4}{2 x-4}=\frac{(x-2)^{2}}{2(x-2)}=\frac{x-2}{2}\end{aligned}$ ‎

Förstagradsekvationer

Om du ska lösa en ekvation måste du få x‐variabeln ensam på ena sidan av likhetstecknet. För att göra detta kan du använda dig av de fyra räknesätten. Du kan använda dem hur du vill bara du gör exakt samma sak på båda sidor.

Plus på båda sidor $x - 5 = 9$ $x - 5 {\color{#96C933} + 5 } = 9 {\color{#96C933} + 5 }$ $x = 14$	Minus på båda sidor $x + 7 = 18$ $x + 7 {\color{#96C933} - 7} = 18 {\color{#96C933} -7 }$ $x = 11$
Dela på båda sidor $3x = 21$ $\frac{3x}{\color{#96C933} 3 } = \frac{21}{\color{#96C933} 3}$ $x = 7$	Multiplicera båda sidor $\frac{x}{2} = 9$ $\frac{{\color{#96C933} 2 \cdot } x}{2} = {\color{#96C933} 2 \cdot } 9$ $x = 18$

Potensekvationer

Innebär att x är upphöjt med ett tal.

T.ex. $x^5 = 243$

Målet är att få x:et fritt. För att få x:et fritt höjer man upp båda sidor med exponentens inverterade värde.

Exempel: $x^5 = 243$ ‎

$(x^5)^{1/5} = 243^{1/5}$ ‎

$x^{5 \cdot \frac{1}{5}} = 243^{1/5}$ ‎

x^1 = 3

Svar: $x=3$

$x^n = C$ ‎

x = C^{1/n}

Kom ihåg:

Vid en potensekvation höjer man upp båda sidor med exponentens inverterade värde.
Om det är en jämn exponent finns det en negativ och en positiv lösning.
Om det är en udda exponent finns det bara en lösning.

Räta linjen

Räta linjens ekvation är $\mathbf{y=kx+m}$

$k =$ linjens lutning
$m =$ skärningspunkt med y-axeln

Två linjer är parallella om $k_{1}=k_{2}$
Två linjer vinkelräta om $k_{1} \cdot k_{2}=-1$

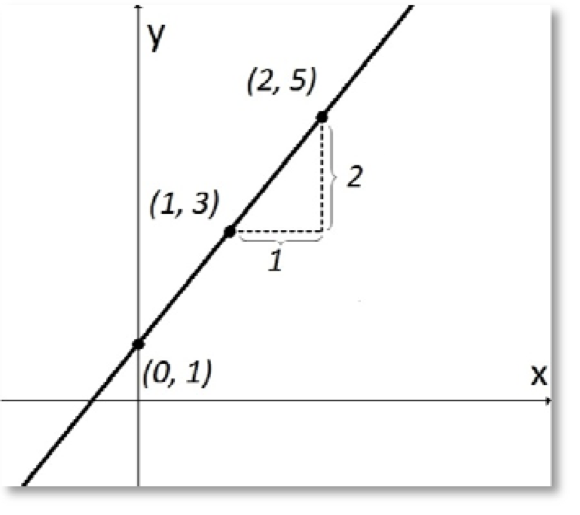
$\begin{aligned}\boldsymbol{k}=\frac{\Delta y}{\Delta x}=\frac{\text { skillnad i y-led}}{\text { skillnad i x-led}}=\frac{5-3}{2-1}=\frac{2}{1}=\mathbf{2}\end{aligned}$ ‎

$\boldsymbol{m}=\text { skärning med } y-\text { axeln }=\mathbf{1}$ ‎

$y=\mathbf{2 x + 1}$ ‎

Från två koordinater till funktion

Linjens lutning, $k$ -värde, fås av: $k=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

Linjära ekvationssystem

Att lösa ett ekvationssystem betyder att man ska finna koordinaten för när linjerna korsar varandra.

Om linjerna

skär varandra har ekvationssystemet en lösning
är parallella har ekvationssystemet inga lösningar
sammanfaller har ekvationssystemet oändligt
många lösningar
Det finns två sätt att lösa ett ekvationssystem algebraiskt (Substitutionsmetoden och additionsmetoden) samt ett sätt att lösa det grafiskt. Det räcker med att kunna en av de algebraiska metoderna.
Substitutionsmetoden är den metod som fungerar även på mer komplicerade ekvationer. Den andra metoden, additionsmetoden, fungerar i vissa fall bra, men överlag är substitutionsmetoden mycket bättre.

Grafisk lösning

Exempel: Lös ekvationssystemet grafiskt: $\left\{\begin{array}{l}y+x=1 \\ y-7=2 x\end{array}\right.$

Vì måste nu rita linjerna. För att göra det måste vi bryta ut $y$ för båda ekvationerna; $\left\{\begin{array}{l}y=-x+1 \\ y=2 x+7\end{array}\right.$

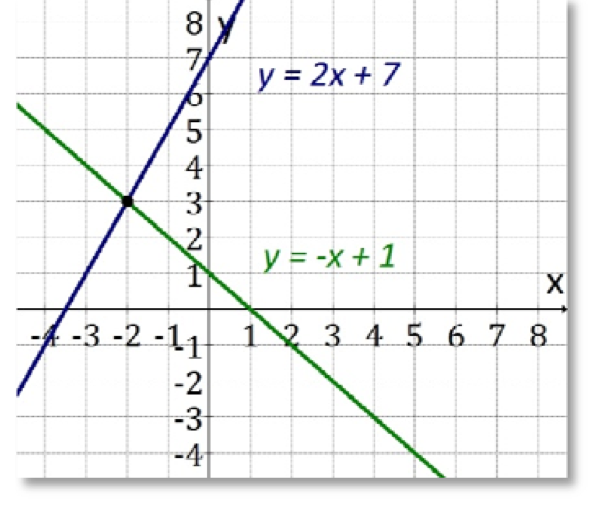
Lösning är vid skärningspunkten, som har koordinaten $(-2,3)$ .

Svar: $\left\{\begin{array}{l}x=-2 \\ y=3\end{array}\right.$

Substitutionsmetoden

Exempel: Lös följande ekvationssystem: $\left\{\begin{array}{c}\color{#96C933}3 y-4 x=17 \\ \color{#3396C9}y-5 x=2\end{array}\right.$

Steg 1: Lös ut antingen $x$ eller $y$ i en av ekvationerna.

\begin{aligned}& \color{#3396C9}y-5 x=2 \\&\color{#3396C9}y=5 x+2\end{aligned}

Steg 2: $\color{#3396C9}y$ är exakt samma sak som $\color{#3396C9}5 x+2$ . Då kan vi byta ut $\boldsymbol{y}$ i den andra ekvationen mot $\color{#3396C9}5 x+2$ .

\begin{aligned} &3 y-4 x=17 \\ &3{\color{#3396C9}(5 x+2)}-4 x=17 \\ &15 x+6-4 x=17 \\ &11 x=11 \\ &x=1 \end{aligned}

Steg 3: Nu vet vi $x$ . Då kan vi räkna ut $y$ .

\begin{aligned} &y=5 x+2 \\ &y=5 \cdot 1+2 \\ &y=7 \end{aligned}

Steg 4: Ekvationssystemet har lösningen $\left\{\begin{array}{l}x=1 \\ y=7\end{array}\right.$

Poängen med metoden är att gå från två ekvationer med två okända variabler (går inte att lösa) till endast en ekvation med en okänd variabel, vilket vi kan lösa.

Lös ut x eller y.
Sätt in uttrycket så du
bara får en okänd.
Sätt in svaret och beräkna den andra.
Svara med x och y.

Andragradsekvationer

Det finns tre olika typer av andragradsekvationer. För varje typ finns det en lösningsmetod.

Andragradsfunktioner – Tillämpningar

Det svåra med att lösa andragradsfunktioner är ofta att tolka frågan. Det finns tre typiska problem. Det gäller att identifiera frågan och därefter använda någon av de tre metoderna nedan.

Exponentialfunktioner

Logaritmer

Definitioner

$\mathbf{\lg 5}$ är det tal $\mathbf{10}$ ska upphöjas med för att det ska bli $\mathbf{5}$ ‎

$\lg 5 \approx 0,7 \rightarrow 10^{0,7} \approx 5 \\ 10^{\lg 5}=5$ ‎

$\begin{aligned} &\lg x=y \leftrightarrow 10^y = x\\ &x=10^{\log x} \end{aligned}$ ‎

Här har vi 10 upphöjt med det tal 10 ska upphöjas med för att det ska bli 5.

Logaritmlagarna

Det finns tre logaritmlagar.

$\log x+\log y=\log x y$
$\log x-\log y=\log \frac{x}{y}$
$\log x^{y}=y \cdot \log x$

Exponentialfunktioner

Exponentialfunktioner innebär att vi har en variabel som exponent. Exponentialfunktioner består vanligtvis av fyra element.

Exponentialfunktioner används för att beskriva kontinuerliga procentuella förändringar.

Geometri

Pythagoras sats

Obs! Gäller endast för rätvinkliga trianglar!

Likformighet

Likformighet innebär att förhållandet mellan två figurers sidor är samma. Det enklaste sättet att ta reda på om två trianglar är likformiga är att kontrollera vinklarna. Om man säkerställer att två vinklar är identiska så är trianglarna likformiga.

Transversalsatsen

Transversalsatsen kan användas när en triangel delas av en parallelltransversal, alltså en linje som är parallell med triangelns bas

Randvinkelsatsen

Randvinkelsatsen ger att en randvinkel alltid är hälften av dess medelpunktsvinkel.

Medelpunktsvinkel är den vinkel man får när man drar två linjer från cirkelns rand till cirkelns mittpunkt. En randvinkel utgår från samma två punkter på randen, men går till en punkt på cirkelns rand.

Statistik

Statistik & Lägesmått

Lägesmått

Det finns tre typer av lägesmått man ska kunna:

$\mathbf{\text{Medelv\"arde}} = \frac{\text{summan av alla v\"arden}}{\text{antalet v\"arden}}$
$\mathbf{\text{Median}} = \text{mittenv\"ardet i en talf\"oljd (i storleksordning)}$
$\mathbf{\text{Typev\"arde}} = \text{v\"ardet som f\"orekommer flest g\aa nger}$

Lådagram – Spridning kring medianen
För att illustrerar en spridning brukar man använda sig av ett lådagram.
Ett lådagram delar upp spridningen i fyra delar. För att rita ett diagram tar man fram största och minsta värde, medianen samt övre och undre kvartil.
Exempel: Ett företag har åtta anställda med följande ålder:

Variationsbredd: största värdet – minsta värdet = 45 – 20 = 25 år.

Kvartilavståndet: övre kvartil – nedre kvartil = 38 – 26 = 12 år.

Varje kvartil motsvarar 25 % av spridningen. Från exemplet ovan kan vi se att spridningen för de 25 % yngsta är mellan 20 och 26 år.

Standardavvikelse – Spridning kring medelvärde

Standardavvikelse kan ses som ett mått på den genomsnittliga avvikelsen från medelvärdet.

För att räkna ut standardavvikelsen tittar man på hur varje värde avviker från medelvärdet. Standardavvikelsen vid ett stickprov beräknas med följande formel:

$\begin{aligned}s_{x}=\sqrt{\frac{\sum(x-\bar{x})^{2}}{n-1}}\end{aligned}$ ‎

$\begin{aligned} &\boldsymbol{s}_{\boldsymbol{x}}=\text { standardavvikelsen } \\ &\sum=\text { summa } \\ &\boldsymbol{x}=\text { observationsv\"arde } \\ &\overline{\boldsymbol{x}}=\text { medelvärdet } \\ &n=\text { antal värden } \end{aligned}$ ‎

Normalfördelning

Normalfördelningskurvan visar hur normalfördelade värden sprider sig kring medelvärdet. Kurvan utgår endast från medelvärdet och standardavvikelsen.